Keyboard shortcuts

Press ← or → to navigate between chapters

Press S or / to search in the book

Press ? to show this help

Press Esc to hide this help

Text Indexing Structures

1. Text Search

We are given an alphabet $\Sigma$ of size $\sigma$, a text string $T$ of length $n$ over $\Sigma$, and a pattern string $p$, we want to find the occurrences of $P$ in $T$.

2. String matching algorithms

  1. No preprocessing
  2. The obvious method: moving window
  3. $O(n + p)$-time solutions T
    • Knuth-Morris-Pratt
    • Boyer-Moore
    • Rabin-Karp

3. Text indexing

  1. Preprocess a $T$-text index
  2. Each time a new pattern is given

4. Warm-up: trie

  1. Representing strings $T_{1}, T_{2}, \dots, T_{k}$
  2. A rooted tree with edges labelled with letters in $\Sigma$
  3. To represent strings as root-to-leaf paths in a trie, terminate them with a new letter $\$$ that is less than any symbol in $\Sigma$ > [!example] > Given ${ ana, ann, anna, anne }$, > > 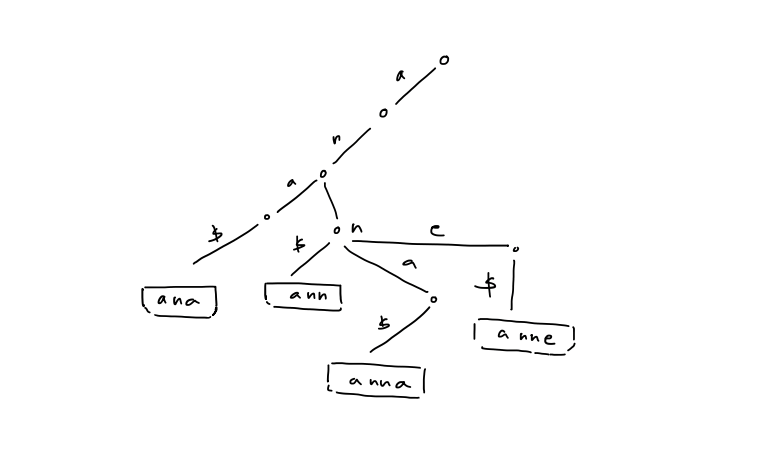Pasted image 20250320135835.png 5. The in-order traversal of leaves is equivalent to a a sorting of the strings in lexicographical order 6. Check if $P$ is in ${ T_{1}, T_{2}, \dots , T_{k} }$ top-down traversal 7. If each node stores pointers to children in sorted order, then the number of nodes in the trie is $\leq \sum_{i=1}^k |T_{i}| + 1$ - Query time: $O(p \log \sigma)$ - Space: $O(n) +$ space form ${ T_{1}, T_{2}, \dots , T_{k} }$ 8. Compressed trie: contract non-branch paths to single edges > [!example] > 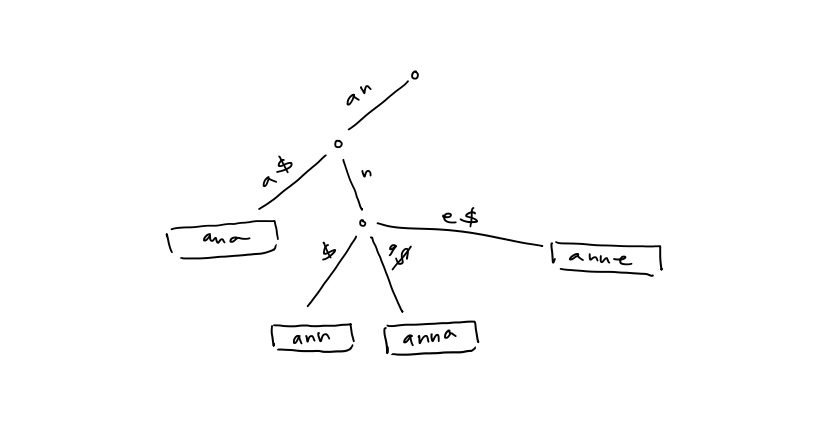Pasted image 20250320135803.png # 5. Suffix Tree 1. A compressed trie of all suffixes of $T \$$ > [!example] > 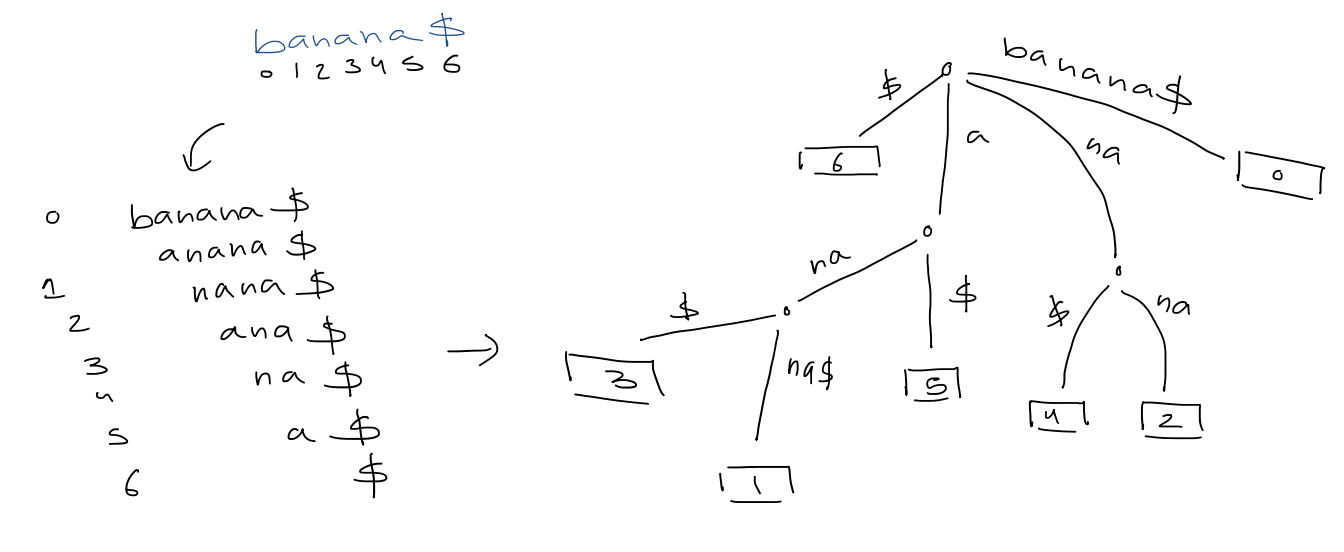Pasted image 20250320135519.png - $n+1$ leaves - Edge label = substring $T[i \dots j]$, store as two indices $(i, j)$ - Space: $O(n)$ 2. Text search - The search for $p$ gives a subtree whose leaves correspond to all occurrences of $p$ - If each node stores pointers to children in sorted order, the query time is $O(p \log \sigma)$ - If we use perfect hashing, the time becomes $O(p)$ - And, if we report all occurrences, the time is $O(p + occ)$ - [ ] #final what if the pattern does match any of the edges exactly (example: n instead of na) 3. Applications - Longest repeating substring in $T$ In $banana \$$, that would be $ana$.

We construct a suffix tree, then look for the branching node of maximum letter depth. When constructing a suffix tree, treat $\sigma$ as a constant, allowing us to bound the construction to $O(n)$ time.

  • #final what does this mean? alphabet

Computing the letter depth in preorder traversal takes $O(n)$ time, too.

  • #final because it uses DFS/BFS right?

6. Suffix array

  1. Sort the suffixes of $T \$$, then just store the indices of the suffixes > [!example] > Note that the entries of the second column are the suffix array > > 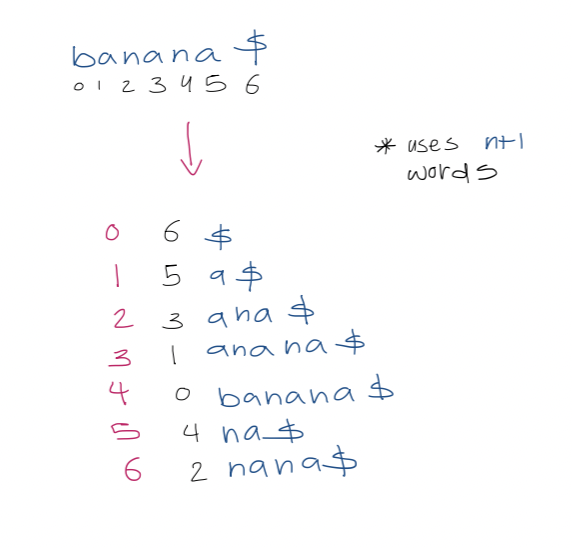Pasted image 20250325133433.png 1. Text search with suffix array We use binary search over the array. This takes $O(\log(n+1)\cdot p)$ to determine where pattern $P$ of length $p$ occurs in $T$. 3. A simple accelerant Let $L, R$ be the left and right boundaries of the current search interval. We use a modified binary search which uses the midpoint to update $L$ or $R$. We also track $l$, the length of the longest prefix of $T[SA[L] \dots n]$ that matches $P$, and $r$, the length of the longest prefix of $T[SA[R] \dots n]$ that matches $P$. > [!example] > For $aba$, > > | $(L,R)$ | $(0,6)$ | $(0,3)$ | $(1,3)$ | $(1,2)$ | > | ------- | -------- | -------- | ------- | ------- | > | $(l,r)$ | $(0, 0)$ | $(0, 1)$ | $(1,1)$ | $(1,1)$ | Define $h$ as $\min(l, r)$. Observe that the first $h$ characters of $P, \ T[S[A] \dots n], \ T[SA[l+1] \dots n], \ \dots, \ T[SA[R] \dots n] \ = \ P[0 \dots h-1]$ So, when comparing in binary search, we can start from $P[h]$. 4. A super accelerant > [!example] > $lcp(2,3) = 3$ We call an examination of a character in $P$ redundant if that character has been examined before. Our goal is to reduce redundant character examination to be $\leq 1$ per iteration of the binary search such that the running time is $O(p + \log n)$ where the $p$ term is due to each non-redundant character examination. To achieve this goal, we need to do more preprocessing first. For each triple $(L, M, R)$ that can arise during binary search, we precompute $lcp(L,M)$ and $lcp(M,R)$. Since there are $(n+1) - 2$ unique midway points. Since there are two arrays indexed by $M$, this uses $2n-2$ total extra space. Let $Pos(i)$ represent the suffix starting at position $T[SA[i] \dots n]$. In the simplest case, in any iteration of the binary search, if $l = r$, then we compare $P$ to the suffix of the midway point $Pos(M)$, starting from $P[h]$, as before. In the general case, when $l \neq r$, we assume w.l.o.g, that $l > r$. We analyze the following three cases: 1. If $lcp(L,M) > l$, then the longest common prefix of suffixes $Pos(L)$ and $Pos(M)$ is larger than the longest common prefix between $P$ and $Pos(L)$. 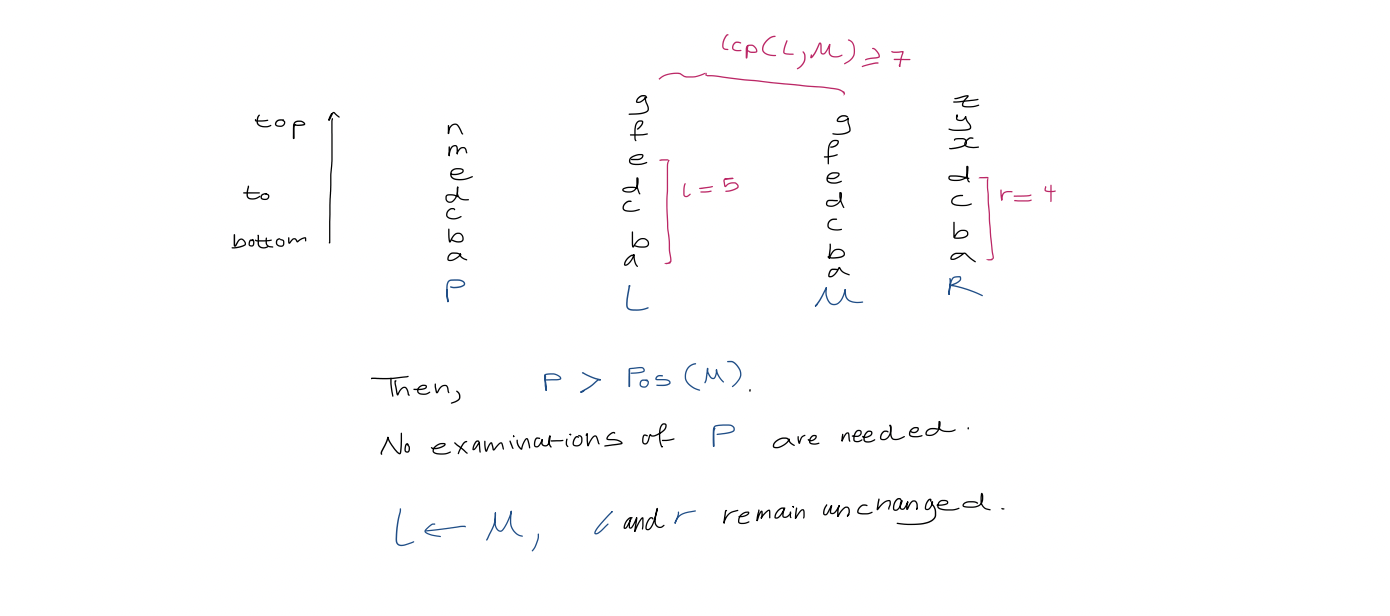Pasted image 20250327134311.png 2. If $lcp(L, M) < l$, Pasted image 20250327134857.png 3. If $lcp(L, M) = l$, then $P$ agrees with $Pos(M)$ up to position $l-1$. Start comparisons from $P[l]$. - [ ] #final so, what happened to L and R here Compare middle, set middle to be left or right boundaries - [ ] #skipped I could probably figure this out if I tried longer ... Running time In the two cases where the algorithm examines a character during the iteration, the comparison starts with $P[\max(l, r)]$. Suppose $k$ characters of $P$ are examined in this iteration. Then there are $k-1$ matches, and $\max(l, r)$ increases by $k-1$. Hence, at the start of any following iteration, $P[\max(l, r)]$ may have already been examined but the next character in $P$ may not have been. Therefore, there are $\leq 1$ redundant character examinations per iteration. Pasted image 20250327140640.png # 7. Construction 1. Suffix trees/arrays for Strings over a constant-sized alphabet can be constructed in $O(n)$ time. 2. Suffix trees/arrays for strings over an alphabet $\Sigma = { 1, 2, 3, \dots , n }$ can also be constructed in $O(n)$ time.

Mentions

  • bzip2